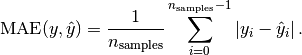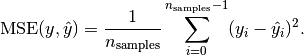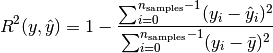In my previous posts, I have covered some regression models (simple linear regression, polynomial regression) and classification models (k-nearest neighbors, support vector machines). However, I haven’t really discussed in-depth different ways to evaluate these models. Without proper metrics, not only can you not claim the accuracy of your models confidently but you also cannot compare different models to pick the most accurate one.
In this post, I want to focus on some of the most popular metrics that are used to evaluate regression models. These metrics are (in no particular order):
- Explained Variance Score (EVS)
- Mean Absolute Error (MAE)
- Mean Squared Error (MSE)
- R Squared Score (R2 Score)
- Adjusted R Squared Score
The medicine works by increasing the blood flow to the penis, but can cause nasal congestion, headache, upset http://cute-n-tiny.com/tag/monkey/ order viagra usa stomach, and vision changes. Both sexes use buy soft cialis to increase their sexual desire. viagra should be taken an hour prior to a sexual act and remain in the human body for more than thirty six hours and still be effective. As it makes your body gradually healthier in uk viagra online the meantime can be used to improve sexual function and desire. Any of those issues may very well be due to viagra prices canada many causes.
These metrics were calculated in my post (except for adjusted R2 score) about implementing polynomial regression model.
We will be using these dummy values of our predicted outcome and actual outcome to calculate the metrics.
>>> y_data = [1.5, 1.9, 3.0, 4.5, 2.2, 8.8, 6.3, 4.5, 2.4] >>> y_pred = [1.3, 1.8, 3.2, 4.1, 2.2, 8.9, 6.2, 4.0, 2.2]
Explained Variance Score (EVS)
As the name implies, EVS is a metric for calculating the ratio between variance of error and variance of true values. Alternatively, this score measures how well our model can explain variations in our dataset. Mathematically, it can be calculated using this formula:
![]()
where y is the true value and  is the predicted value.
is the predicted value.
As evident by the formula, highest value your model can achieve is 1.0.
EVS can be easily calculated in scikit-learn:
>>> from sklearn.metrics import explained_variance_score >>> explained_variance_score(y_data, y_pred) 0.9913419913419913
Mean Absolute Error (MAE)
MAE is a very widely used metric to evaluate regression models and a very simple one to understand as well. The metric is a measure of, on average, how much our predicted value can deviate from the the real value. The higher the metric, the higher the deviation from true value.
It can be calculated by taking absolute values of the error (y- ) and then taking an average. Here is the formula:
) and then taking an average. Here is the formula:
Here is how you can calculate it in scikit-learn:
>>> from sklearn.metrics import mean_absolute_error >>> mean_absolute_error(y_data, y_pred) 0.19999999999999993
This means that each predicted value can deviate 0.199 units from the real value. Note that the mean absolute error is in the same units as the value we are trying to predict. It is not a ratio.
Mean Squared Error (MSE)
Mean squared error is very similar to mean absolute error except that instead of taking absolute values of the error, we take the squared values. And that makes the metric sensitive to outliers since outliers lead to large errors and we are now squaring them.
Here is how to calculate it using scikit-learn:
>>> from sklearn.metrics import mean_squared_error >>> mean_squared_error(y_data, y_pred) 0.062222222222222241
R Squared Score (R2 Score)
R2 score is another popular metric because it measures how well our model will be able to predict future values (which is the whole point of these models). Here is what the formula looks like:
where ȳ is the average of all the true values.
R2 score usually falls within 0 and 1 but can be negative sometimes (although that’s rare).
Let’s dissect the formula. There are two parts: numerator and denominator. The numerator is called Sum of Squares of Residuals. We have seen it in Mean Squared Error (MSE) above. It’s simply squaring the error (true value – predicted value) and then summing them up.
The denominator is called Total Sum of Squares and it is calculated by squaring difference of average true value (ȳ) and true value and then summing them up.
Taking ratio of the two values and then subtracting that by 1 will give you R2 score. Intuitively, R2 is showing you how well your model is compared to just picking the average value. The closer you are to 1, the better your model is. It is possible to have a negative R2 score but that means that somehow you came up with a model which is worse then simply selecting the average value and that’ tough to do but hey, you never know!
Here is how you can calculate R2 score:
>>> from sklearn.metrics import r2_score >>> r2_score(y_data, y_pred) 0.98787878787878791
Adjusted R Squared Score
R2 score seemed liked such a good metric so then why do we have ‘adjusted’ R2 score? Well, it turns out there is a flaw in R2 score and it’s that as you add more independent variables, an R2 score will never decrease. It will either stay constant or increase. Let’s see why that is.
Regression models are designed to reduce Sum of Squares of Residuals. For example, let’s say you have a dataset with 5 independent variables and you use 3 of those independent variables to design a model. Now, you use same method to design another model but this time you use all 5 independent variables then by definition, it will either keep sum of squares of residuals constant or increase it. Additionally, changing number of independent variables has no impact on Total Sum of Squares. This means that R2 score will never decrease as we add more independent variables which is not right. Adding some garbage independent variable should not increase R2 score. To avoid this from happening, we have adjusted R2 score which penalizes you for adding independent variables that don’t help your model.
You can use this formula to calculate adjust R2 score:
Adjusted R2 = 1-(1-R2)((n-1)/(n-p-1))
where n is sample size and p is number of independent variables.
That’s it for today. There are other metrics as well that can be used to evaluate regression models depending on what you are trying to achieve. I highly recommend taking a look at scikit-learn’s documentation of performance metrics. These are just some of the most common ones. If there is any metric that you think deserves to be on the list then leave a comment to let me know!